واژه عدد اول

عدد اول، این مفهوم جذاب و بنیادین در ریاضیات، همواره مورد توجه ریاضیدانان و پژوهشگران بوده است. در حالی که اعداد طبیعی ما را در زندگی روزمره احاطه کرده‌اند، اعداد اول به عنوان کلیدهای بازگشایی رازهای عددی و الگوریتم‌های پیچیده عمل می‌کنند. در ادامه همراه با راوی پدیا باشید.

آیا تا به حال فکر کرده‌اید که چرا این اعداد با ویژگی‌های منحصر به فردشان در زمینه‌هایی چون رمزنگاری و امنیت اطلاعات این‌قدر اهمیت دارند؟ در حقیقت، اعداد اول به دلیل خواص خاص خود، نقش مهمی در بسیاری از حوزه‌های علمی و فناوری ایفا می‌کنند و می‌توانند به ما در درک بهتر ساختارهای ریاضیاتی کمک کنند.

در این مقاله، به بررسی عمیق عدد اول، ویژگی‌های آن و کاربردهای گسترده‌اش خواهیم پرداخت. از تاریخچه اعداد اول و تأثیر آنها بر نظریه‌های ریاضیاتی گرفته تا نقش آنها در فناوری‌های مدرن، هر جنبه‌ای را با دقت بررسی می‌کنیم. با آشنایی با این اعداد، درک بهتری از ساختارهای ریاضیاتی و کاربردهای علمی و عملی آنها خواهید داشت. همچنین، در این مسیر، ما به مشکلات و سؤالات حل‌نشده‌ای که همچنان در این زمینه وجود دارد خواهیم پرداخت و به بررسی چگونگی تأثیرگذاری این سؤالات بر پیشرفت‌های ریاضی و تکنولوژیک خواهیم پرداخت.

درک عدد اول

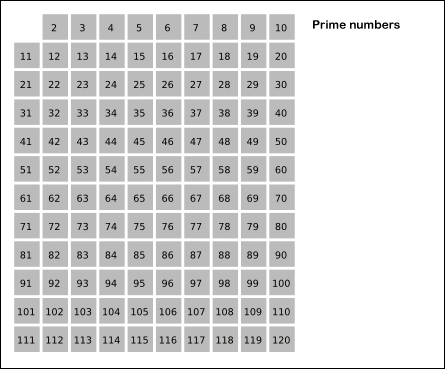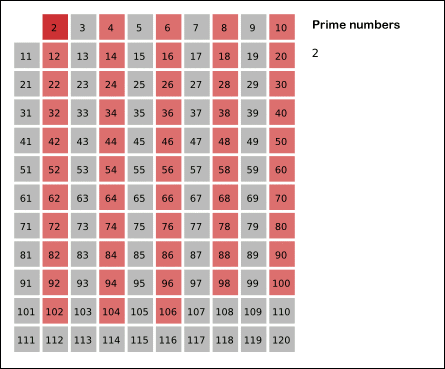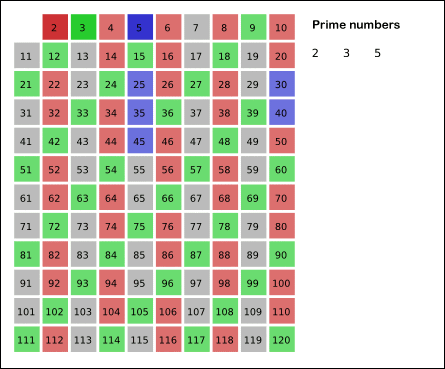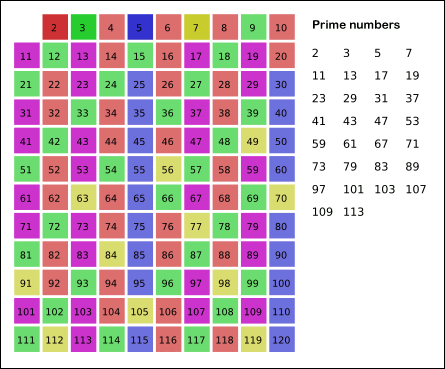
عدد اول، یکی از مفاهیم بنیادی و مهم در نظریه اعداد است. این عدد طبیعی بزرگ‌تر از ۱ است که نمی‌توان آن را به‌صورت ضرب دو عدد طبیعی کوچک‌تر نوشت. به عبارت دیگر، عدد اول فقط بر خود و یک بخش‌پذیر است. به عنوان مثال، عدد ۷ یک عدد اول است زیرا تنها بر ۱ و ۷ تقسیم‌پذیر است. در مقابل، عددی مانند ۶ عددی مرکب است، چرا که می‌توان آن را به‌صورت ۲ × ۳ نوشت که هردوی این اعداد از ۶ کوچک‌ترند. به همین ترتیب، هر عددی که نتوان آن را به صورت حاصل‌ضرب دو عدد طبیعی کوچک‌تر نوشت، به عنوان عدد اول شناخته می‌شود.

یکی از نکات جالب در مورد اعداد اول این است که تعداد آنها بی‌نهایت است. این موضوع توسط ریاضیدانان قدیمی مانند اقلیدس ثابت شده است و همچنان موضوعی جذاب برای پژوهش‌های ریاضیاتی محسوب می‌شود. اعداد اول نه تنها در ریاضیات، بلکه در حوزه‌های مختلفی مانند علوم کامپیوتر و رمزنگاری نیز کاربرد دارند. در واقع، بسیاری از الگوریتم‌های رمزنگاری برای امنیت داده‌ها به سختی تجزیه اعداد بزرگ به عوامل عدد اولشان متکی هستند. این وابستگی به اعداد اول، نشان‌دهنده‌ی اهمیت این اعداد در حفظ اطلاعات و امنیت داده‌ها است. بنابراین، شناخت و درک اعداد اول برای هر فردی که به دنیای ریاضیات و علوم کامپیوتر علاقه‌مند است، امری ضروری به شمار می‌رود.

کاربردهای عدد اول در دنیای مدرن به حدی گسترش یافته است که می‌توان گفت که فهم درست و کامل این اعداد به دانش‌آموزان و پژوهشگران کمک می‌کند تا درک بهتری از ساختارهای ریاضیاتی و الگوریتم‌های پیچیده داشته باشند. از این رو، منابعی مانند راوی پدیا به عنوان یک دانشنامه مجازی، می‌توانند راهنمای خوبی برای یادگیری عمیق‌تر در این زمینه باشند. این منابع می‌توانند به بررسی سؤالات مختلف و مفاهیم پیچیده‌تری که به اعداد اول مربوط می‌شود، کمک کنند و به همین دلیل، برای یادگیری و پژوهش در این حوزه بسیار مفید هستند.

ویژگی‌های عدد اول

ویژگی‌های عدد اول به وضوح آنها را از سایر اعداد متمایز می‌کند. از جمله این ویژگی‌ها می‌توان به موارد زیر اشاره کرد: اولین ویژگی این است که عدد اول تنها بر خود و ۱ بخش‌پذیر است. این خاصیت اصلی عدد اول است. به عنوان مثال، عدد ۵ تنها بر ۱ و ۵ بخش‌پذیر است و نمی‌توان آن را به‌صورت حاصل‌ضرب دو عدد طبیعی کوچک‌تر از خود نوشت. دومین ویژگی، مثبت بودن اعداد اول است. اعداد اول همیشه مثبت هستند. برای مثال، عدد ۳ دارای دو ضریب ۱ و ۳ است، در حالی که عدد منفی ۳ نمی‌تواند به‌عنوان عدد اول در نظر گرفته شود.

سومین ویژگی، بزرگ‌تر بودن عدد اول از ۱ است. عدد اول باید بزرگ‌تر از ۱ باشد، زیرا تنها ضریب عدد ۱ خودش است و نمی‌توان آن را به‌عنوان عدد اول در نظر گرفت. چهارمین ویژگی، فرد بودن اعداد اول است. به جز عدد ۲ که تنها عدد اول زوج است، تمام اعداد اول دیگر فرد هستند. این بدان معناست که اعداد زوج معمولاً بیش از دو ضریب دارند و به همین دلیل نمی‌توانند عدد اول باشند. این ویژگی‌ها نه تنها در تعریف عدد اول مهم هستند، بلکه در تجزیه و تحلیل و شناسایی اعداد اول به‌کار می‌روند. برای شناسایی یک عدد اول، روش‌های مختلفی وجود دارد، از جمله آزمون تقسیم و الگوریتم‌های پیچیده‌تر مانند آزمون میلر-رابین.

کاربردهای عدد اول

عدد اول در حوزه‌های مختلف علمی و فناوری کاربردهای فراوانی دارد. یکی از مهم‌ترین کاربردهای اعداد اول در رمزنگاری است. در دنیای دیجیتال امروز، امنیت اطلاعات یکی از بزرگ‌ترین چالش‌ها محسوب می‌شود. الگوریتم‌های رمزنگاری کلید عمومی، مانند RSA، به سختی تجزیه اعداد بزرگ به عواملی عدد اول متکی هستند. این بدان معناست که اگر کسی بخواهد اطلاعات رمزنگاری‌شده را بشکند، باید بتواند این اعداد را تجزیه کند، که این کار به دلیل پیچیدگی محاسباتی بسیار دشوار است. به همین دلیل، اعداد اول به عنوان ابزارهای کلیدی در امنیت اطلاعات شناخته می‌شوند و پژوهش در زمینه آنها همچنان ادامه دارد.

علاوه بر این، اعداد اول در نظریه‌های عددی و تحقیقات علمی نیز به کار می‌روند. برای مثال، حدس گلدباخ که بیان می‌کند هر عدد صحیح زوج بزرگ‌تر از ۲ را می‌توان به‌صورت جمع دو عدد اول بیان کرد، یکی از مسائل مشهور و حل‌نشده در ریاضیات است. همچنین، اعداد اول دوقلو (اعدادی که تنها دو واحد از یکدیگر فاصله دارند) نیز توجه بسیاری از ریاضیدانان را به خود جلب کرده است. این تحقیقات در زمینه اعداد اول، به پیشرفت‌های بیشتری در علوم ریاضی و کامپیوتر کمک کرده و می‌تواند به توسعه الگوریتم‌های جدید منجر شود.

اعداد اول معروف

در دنیای ریاضیات، تعدادی عدد اول وجود دارد که به دلیل ویژگی‌های خاص یا کاربردهایشان بسیار معروف هستند. به عنوان مثال، عدد ۲ به عنوان کوچک‌ترین و تنها عدد اول زوج شناخته می‌شود. سپس عدد ۳ به عنوان اولین عدد اول فرد به شمار می‌رود. در ادامه، اعداد اول معروف دیگری مانند ۵، ۷، ۱۱ و ۱۳ وجود دارند که به‌طور گسترده در مسائل ریاضی مورد استفاده قرار می‌گیرند. این اعداد به دلیل ویژگی‌های خاص خود، در نظریه اعداد و الگوریتم‌های مختلف به کار می‌روند و می‌توانند به درک بهتر ساختارهای ریاضی کمک کنند.

علاوه بر این، اعداد مرسن که به فرم ۲^p – 1 هستند (که در آن p خود عدد اولی است) نیز بسیار معروف هستند. بزرگ‌ترین عدد اول شناخته‌شده که در سال ۲۰۱۸ کشف شد، یک عدد مرسن بود که ۲۲,۳۳۸,۶۱۸ رقم دارد. این عدد در جریان پروژه‌ای به نام “تحقیق اینترنتی بزرگ عدد مرسن” (GIMPS) به‌دست آمده است. این اعداد نه تنها در نظریه اعداد، بلکه در علوم کامپیوتر و فناوری اطلاعات نیز کاربرد دارند. بنابراین، آشنایی با این اعداد و ویژگی‌هایشان می‌تواند به پژوهشگران و علاقه‌مندان به ریاضیات کمک کند تا درک بهتری از دنیای ریاضیاتی پیدا کنند.

اهمیت عدد اول

اهمیت عدد اول فراتر از صرفاً یک مفهوم ریاضی است. این اعداد به عنوان بلوک‌های سازنده برای اعداد طبیعی عمل می‌کنند و در بسیاری از نظریه‌ها و الگوریتم‌ها در حوزه‌های مختلف علمی و فناوری به کار می‌روند. در واقع، اعداد اول به‌عنوان ابزارهایی برای فهم بهتر ساختار عددها و روابط میان آنها به شمار می‌آیند. این ویژگی‌ها آنها را به یکی از موضوعات جذاب در ریاضیات تبدیل کرده و همچنان محققان را به خود جلب می‌کنند.

در دنیای دیجیتال، امنیت اطلاعات به شدت به اعداد اول وابسته است. رمزنگاری کلید عمومی، که در ارتباطات آنلاین و انتقال اطلاعات حساس به کار می‌رود، به شدت به سختی تجزیه اعداد بزرگ به عوامل عدد اول وابسته است. این به معنای آن است که اعداد اول نقش حیاتی در حفاظت از اطلاعات و امنیت داده‌ها دارند. به همین دلیل، شناخت و درک عمیق‌تر از اعداد اول برای هر فردی که در زمینه‌های مرتبط با فناوری و امنیت اطلاعات فعالیت می‌کند، ضروری است.

کشف دنیای جذاب اعداد اول

در این مقاله، ما به عمق مفهوم عدد اول پرداخته و ویژگی‌ها و کاربردهای آن را در دنیای ریاضیات و فناوری‌های مدرن بررسی کردیم. اعداد اول به عنوان پایه‌های اساسی در نظریه عددی و رمزنگاری، نقشی کلیدی در امنیت اطلاعات و ساختارهای ریاضیاتی ایفا می‌کنند. با توجه به بی‌نهایت بودن این اعداد و جذابیت‌های پژوهشی حول آن‌ها، به‌نظر می‌رسد که همچنان در آینده، تحقیقات در این زمینه ادامه خواهد داشت. این تحقیقات می‌تواند به کشف الگوها و روابط جدید میان اعداد اول منجر شود و به پیشرفت‌های بیشتری در زمینه‌های مرتبط کمک کند.

علاوه بر این، اهمیت اعداد اول فراتر از یک مفهوم تئوری است؛ آن‌ها به ما کمک می‌کنند تا درک بهتری از دنیای عددها و روابط میان آن‌ها پیدا کنیم. منابع معتبر و آموزشی مانند راوی پدیا، به عنوان ابزارهایی برای یادگیری و پژوهش در این حوزه، می‌توانند به دانش‌آموزان و پژوهشگران در کشف و فهم عمیق‌تر این مقوله کمک کنند. این منابع می‌توانند به عنوان پل ارتباطی بین علاقه‌مندان به ریاضیات و دنیای پیچیده اعداد اول عمل کنند و به گسترش دانش علمی در این زمینه کمک کنند.

در نهایت، ارتباطات میان اعداد اول و فناوری‌های نوین نشان‌دهنده اهمیت این اعداد در زندگی روزمره ماست. با ادامه تحقیقات و کشفیات جدید، می‌توان به دنیای شگفت‌انگیز اعداد اول بیشتر و بیشتر نزدیک شد و به درک عمیق‌تری از ساختارهای ریاضیاتی و الگوریتم‌های پیچیده دست یافت. این سفر به دنیای اعداد اول، نه تنها ما را با مفاهیم جدید آشنا می‌کند، بلکه ما را به چالش‌هایی فراتر از آنچه که تاکنون درک کرده‌ایم، سوق می‌دهد و به ما این امکان را می‌دهد که با نگاهی نو به ریاضیات و علم کامپیوتر بنگریم.