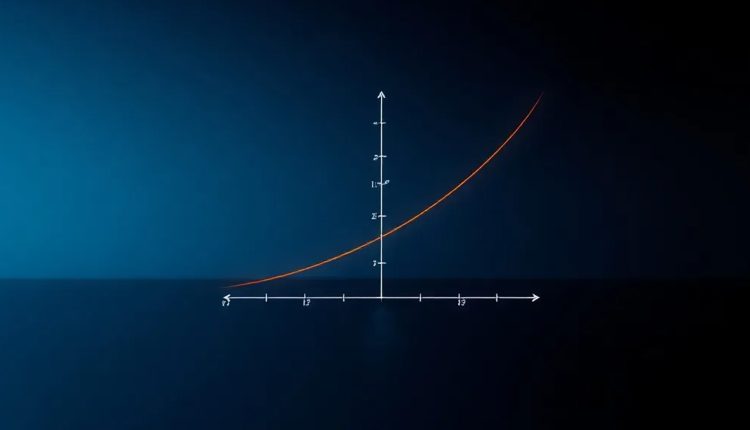
واژه تابع در ریاضیات

تابع در ریاضیات یکی از مفاهیم کلیدی است که به ما کمک می‌کند تا روابط پیچیده بین مجموعه‌ها را به سادگی درک کنیم. آیا تا به حال به این فکر کرده‌اید که چگونه می‌توانیم با استفاده از یک قاعده مشخص، از یک عدد به عدد دیگری برسیم؟ در ادامه همراه با راوی پدیا باشید.

این همان کاری است که تابع انجام می‌دهد. از توصیف روابط اقتصادی گرفته تا تحلیل رفتارهای طبیعی، توابع به ما امکان می‌دهند تا دنیای اطراف خود را با دقت بیشتری مدل‌سازی کنیم. در واقع، توابع به عنوان ابزاری برای تبیین و بررسی پدیده‌های مختلف در دنیای واقعی به کار می‌روند و ما را قادر می‌سازند تا الگوها و روندهای موجود در داده‌ها را شناسایی کنیم.

در این مقاله به بررسی مفهوم تابع، واژه‌شناسی آن و انواع مختلف توابع خواهیم پرداخت. همچنین به تاریخچه و ویژگی‌های این مفهوم ریاضی خواهیم پرداخت که به ما کمک می‌کند تا درک بهتری از کاربردهای آن در رشته‌های مختلف پیدا کنیم.

با ما همراه باشید تا در دنیای جذاب توابع و کاربردهای آن‌ها در ریاضیات و علوم بپردازیم و ببینیم چگونه این ابزارها می‌توانند به ما در حل مسائل روزمره و علمی کمک کنند. به طور خاص، هدف ما این است که روشن کنیم چگونه توابع می‌توانند ابزاری برای حل مسائل پیچیده در زندگی روزمره و همچنین در حوزه‌های علمی مانند فیزیک و اقتصاد باشند.

تابع در ریاضیات

تابع در ریاضیات، یک مفهوم اساسی است که به توصیف روابط بین مجموعه‌ها می‌پردازد. در واقع، تابع یک رابطه دوتایی است که هر عنصر از مجموعه ورودی را به یک عنصر از مجموعه خروجی مرتبط می‌کند. به عنوان مثال، اگر مجموعه X شامل اعداد طبیعی باشد و مجموعه Y شامل اعداد صحیح، تابع f می‌تواند هر عدد طبیعی x را به عدد صحیحی y نسبت دهد، به طوری که هر عدد ورودی تنها به یک عدد خروجی مرتبط باشد. این ویژگی، تابع را از سایر روابط متمایز می‌کند و به آن اجازه می‌دهد تا به عنوان یک ابزار ریاضی قوی در حل مسائل مختلف مورد استفاده قرار گیرد. به همین دلیل، توابع در تحلیل و مدلسازی داده‌ها نقش بسزایی دارند و به ما کمک می‌کنند تا روابط میان متغیرها را بهتر درک کنیم.

واژه تابع در ریاضیات

واژه تابع در ریاضیات، به معنای یک رابطه بین دو مجموعه است که به هر عضو از مجموعه اول (دامنه) یک عضو از مجموعه دوم (برد) نسبت می‌دهد. به طور کلی، اگر f یک تابع باشد، می‌توان آن را به صورت f: X → Y نشان داد، به طوری که X دامنه و Y برد تابع است. در این راستا، برای هر x در X، مقدار تابع f در x با f(x) نمایش داده می‌شود. این ارتباط میان ورودی و خروجی، به نوعی نشان‌دهنده یک قانون یا قاعده است که بر اساس آن می‌توان مقدار خروجی را از ورودی محاسبه کرد. به عبارت دیگر، تابع به ما امکان می‌دهد تا با استفاده از قوانین مشخص، ارتباطات میان متغیرهای مختلف را تحلیل کنیم و نتایج را پیش‌بینی کنیم.

معنی تابع در ریاضیات

معنی تابع در ریاضیات به نوعی به ارتباط میان عناصر مختلف اشاره دارد. به عبارت دیگر، تابع یک رابطه دوتایی است که برای هر عنصر از مجموعه ورودی، یک عنصر منحصر به فرد در مجموعه خروجی مشخص می‌کند. این ویژگی باعث می‌شود که تابع بتواند به عنوان ابزاری موثر در حل مسائل ریاضی و توصیف پدیده‌های مختلف استفاده شود. به عنوان مثال، در مسائل اقتصادی، تابع می‌تواند به توصیف رابطه بین هزینه و درآمد کمک کند. همچنین، در زمینه‌های علمی دیگر، مانند فیزیک، تابع می‌تواند به توصیف رفتارهای مختلف سیستم‌ها و پدیده‌ها کمک کند و بدین ترتیب درک بهتری از روندها و الگوهای موجود در داده‌ها فراهم کند.

تعریف تابع

تعریف تابع در ریاضیات به صورت دقیق به این صورت است: یک تابع از مجموعه X به مجموعه Y از طریق قاعده‌ای مشخص می‌شود که هر عنصر x در X را به یک عنصر منحصر به فرد y در Y نسبت می‌دهد. به عبارت دیگر، هیچ دو عنصر x در X نمی‌توانند به یک عنصر y در Y مرتبط شوند. این تعریف به وضوح نشان می‌دهد که تابع می‌تواند به عنوان یک قاعده برای تناظر بین اعضای دو مجموعه در نظر گرفته شود. با توجه به این تعریف، توابع می‌توانند به صورت ریاضیاتی یا گرافیکی نمایش داده شوند و این توانایی به ما این امکان را می‌دهد که به راحتی رفتار آن‌ها را تحلیل کنیم و تغییرات را شبیه‌سازی کنیم.

انواع تابع

انواع تابع در ریاضیات بسیار متنوع و گسترده است. می‌توان توابع را بر اساس ویژگی‌های مختلفی دسته‌بندی کرد. برخی از انواع معروف توابع شامل توابع چندجمله‌ای، توابع مثلثاتی، توابع نمایی و لگاریتمی، توابع قدر مطلق و توابع همانی هستند. هر یک از این توابع دارای ویژگی‌ها و کاربردهای خاص خود هستند و در زمینه‌های مختلف ریاضی و علوم کاربردی مورد استفاده قرار می‌گیرند. برای مثال، توابع مثلثاتی در هندسه و توابع نمایی در مسائل مالی و جمعیت‌شناسی کاربرد فراوان دارند. همچنین، توابع لگاریتمی به ما امکان می‌دهند تا به راحتی نرخ تغییرات را محاسبه کنیم و در تحلیل داده‌ها مفید باشند.

کاربرد تابع

کاربرد تابع در ریاضیات و علوم مختلف بسیار گسترده است. به عنوان مثال، در فیزیک، بسیاری از پدیده‌ها مانند حرکت اجسام و تغییرات دما به صورت تابعی از زمان توصیف می‌شوند. همچنین در اقتصاد، تابع می‌تواند به توصیف رابطه میان عرضه و تقاضا کمک کند. در علوم رایانه، توابع به عنوان واحدهای اساسی در برنامه‌نویسی و الگوریتم‌ها مورد استفاده قرار می‌گیرند. به طور کلی، تابع یک ابزار مهم است که می‌تواند به تحلیل و توصیف روابط پیچیده بین داده‌ها و متغیرها کمک کند. این ویژگی‌ها باعث می‌شود که توابع به عنوان ابزاری کلیدی در بسیاری از حوزه‌های علمی و مهندسی شناخته شوند و در حل مسائل کاربردی مورد استفاده قرار گیرند.

تاریخچه تابع

تاریخچه تابع به دوران باستان برمی‌گردد، اما مفهوم مدرن آن در قرن هفدهم و هجده میلادی شکل گرفت. ریاضیدانانی مانند دکارت و نیوتن نقش مهمی در توسعه مفهوم تابع ایفا کردند. با گذشت زمان، مفهوم تابع به یکی از ارکان اصلی ریاضیات تبدیل شد و به توسعه نظریه‌های پیچیده‌تری مانند تحلیل ریاضی و نظریه توابع کمک کرد. امروزه، تابع به عنوان یک مفهوم کلیدی در بسیاری از شاخه‌های ریاضیات و علوم کاربردی شناخته می‌شود. این تاریخچه نشان‌دهنده اهمیت و تأثیر تابع در توسعه علوم مختلف است و به ما کمک می‌کند تا درک بهتری از فرآیندهای ریاضی و کاربردهای آن‌ها پیدا کنیم.

ویژگی‌های تابع

ویژگی‌های تابع شامل دامنه، برد، پیوستگی و یکنوایی است. دامنه تابع مجموعه‌ای از مقادیر ورودی است که تابع بر اساس آن عمل می‌کند، در حالی که برد مجموعه‌ای از مقادیر خروجی است که تابع می‌تواند تولید کند. پیوستگی به این معناست که تابع در هر نقطه‌ای از دامنه خود مقدار مشخصی دارد و یکنوایی به این معناست که برای هر مقدار ورودی، تنها یک مقدار خروجی وجود دارد. این ویژگی‌ها به درک بهتر رفتار توابع و تحلیل آن‌ها در مسائل مختلف کمک می‌کند. همچنین، آگاهی از این ویژگی‌ها می‌تواند به ما در پیش‌بینی نتایج و تحلیل داده‌ها کمک کند و به ما اجازه دهد تا روابط میان متغیرها را به دقت بررسی کنیم.

جمع‌بندی

مفهوم تابع در ریاضیات به عنوان یک ابزار اساسی، نقش کلیدی در درک روابط پیچیده بین مجموعه‌ها ایفا می‌کند. این مفهوم توانسته است به ما کمک کند تا با استفاده از قواعد مشخص، از ورودی‌ها به خروجی‌های منحصر به فرد برسیم و در نتیجه، دنیای اطراف خود را بهتر مدل‌سازی کنیم. توابع نه تنها در ریاضیات، بلکه در علوم مختلفی نظیر فیزیک، اقتصاد و علوم کامپیوتر به کار گرفته می‌شوند و به تحلیل و توصیف پدیده‌ها و روابط پیچیده کمک می‌کنند. با بررسی تاریخچه، انواع و ویژگی‌های تابع، می‌توانیم به درکی عمیق‌تر از این مفهوم برسیم و کاربردهای گسترده آن را در زندگی روزمره و علمی مشاهده کنیم.